Closed-Form Logit Steering

COLLINS WESTNEDGE
OCT 8, 2025

Goal

The goal is to derive the closed-form minimal perturbation to an input x that achieves any target probability p ∈ (0,1) in logistic regression.

Identities & Intuition

Model components

• Sigmoid: \(\sigma(z)=\dfrac{1}{1+e^{-z}}\)
  maps score to probability (e.g., \(z=0 \Rightarrow p=0.5\))

• Score: \(z=w^T x + b\)
  linear combination of features plus bias term

• Logit (log-odds): \(\operatorname{logit}(p)=\ln\!\left(\dfrac{p}{1-p}\right)\)
  maps probability to linear score (inverse of \(\sigma\))

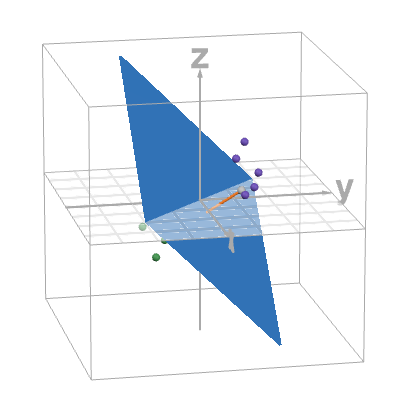
Geometry

• \(H=\{\,x\in\mathbb{R}^n:\; w^T x + b = 0\,\}\) — decision boundary (\(p=0.5\))
  
• \(w \perp H\) — \(w\) is normal to \(H\)

Approach

Move \(x\) along \(w\) by some \(\lambda\):

\[ x' = x + \lambda w \] with \[ \operatorname{logit}(p) = w^T x' + b. \]

Derivation

1. Set up the constraint: Since the model’s score is \(z = w^T x' + b\) and we want probability \(p\), we require \(w^T x' + b = \operatorname{logit}(p)\).

2. Plug in \(x'\) (use \(w^T w=\|w\|^2\)):

\[ \begin{aligned} \operatorname{logit}(p) &= w^T(x+\lambda w)+b \\ &= w^T x + \lambda\, w^T w + b \\ &= w^T x + \lambda\|w\|^{2} + b. \end{aligned} \]

3. Solve for \(\lambda\):

\[ \lambda = \frac{\operatorname{logit}(p) - (w^T x + b)}{\|w\|^{2}}. \]

4. Substitute \(\lambda\) into \(x' = x + \lambda w\):

\[ x' = x + \frac{\operatorname{logit}(p) - (w^T x + b)}{\|w\|^{2}}\,w. \]

Final Formula

\[ \boxed{ x' = x + \frac{\operatorname{logit}(p) - (w^T x + b)}{\|w\|^{2}}\,w } \]

Where \(x' = x + \lambda w\) achieves the target probability \(p\).

Interactive Demo

Open interactive visualization →

Applications

• counterfactual creation ?
  
• debiasing / concept erasure ✓
  
• hard negative mining ✓